Using math to predict how cancer progresses in the human body
July 10, 2017
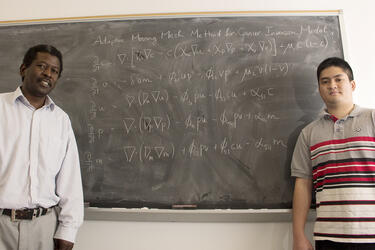
July 10, 2017
Mathematics and Statistics' Assistant Professor Mohamed Sulman, Ph.D. and his doctoral student, Truong Nguyen are investigating mathematical models that describe cancer cells invasion of a biological tissue.
Sulman examines mathematical models simulating cancer cells invasion of the extracellular matrix (ECM). The invasion is driven by the cancer cells movement as a result of their interactions with the proteins in the ECM, their diffusion, the gradients of the chemicals (chemotaxis) within the ECM and the gradient in the structure of the ECM.
The models describing the dynamics of cancer cell
Finding the right college means finding the right fit. See all that the College of Science and Math has to offer by visiting campus.